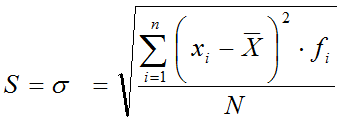Resumen Temas 14 al 17: Visión general de las TICs. TICs y salud. Cuidados 2.0.

Las Tecnologías de la Información y la Comunicación (TICs) han pasado a formar parte de la vida de las personas. Cada vez se usan mas y se incorporan a diferentes ámbitos del día a día (trabajo, entretenimiento, investigación...). Su uso puede ser adecuado, aunque también inadecuado.

• Tecnología de la Comunicación: radio, televisión y teléfono.
• Tecnología de la Información: caracterizada por la digitalización de la tecnología: informática y telemática.

Las TICs nos permiten crear, transformar, almacenar, gestionar, recuperar y difundir información de forma rápida, así como comunicarnos casi instantáneamente.

Ventajas del uso de las TICs sobre la sociedad:

• Desarrollo económico y social.
• Nuevos empleos.
• Nuevos modos de atención de salud.
• Avance de las ciencias.
• Oportunidades comerciales.

Entre otros.

Mediante los siguientes aspectos, las TICs elevan la calidad de asistencia sanitaria:

• Mejorar los procesos asistenciales.
• Los ciudadanos tienen mejor acceso a los servicios, sin que el espacio o el tiempo sean un problema.
• Agiliza los procesos burocráticos.
• Facilita la colaboración de los profesionales entre ellos y con los pacientes.
• Proporciona el máximo de información de ciudadanía para las distintas redes.

1. Áreas de las TICs.

- 1999: La UE establece e-Europe para hacer llegar a los ciudadanos los beneficios de la sociedad del conocimiento.

- 2000: La UE estableció 11 áreas de las TICs entre las que se encuentran la e-Salud, y dentro de esa área, 5 eran áreas de las TICs sanitarias que garantizaban la cobertura y el desaceleramiento del gasto sanitario:

• La historia clínica electrónica (HCE).
• Receta electrónica
• Movilidad
• Telemedicina
• Picture Archiving Communication System (PACS).

2. e-salud.

“La ciber-salud es el apoyo que la utilización costo-eficaz y segura de las tecnologías de la información y las comunicaciones, ofrece a la salud y a los ámbitos relacionados con ella, con inclusión de los servicios de atención de salud, la vigilancia y la documentación sanitarias, así como la educación, los conocimientos y las investigaciones en materia de salud”- OMS, documento de Estrategia y Plan de Acción sobre e-salud, 2011.

Conceptos importantes:

• Historia Clínica Electrónica (HCE): Para identificar pacientes a través de la tarjeta sanitaria en cualquier centro de salud.
• Receta electrónica: Se prescribe en la tarjeta sanitaria para que la compra se pueda realizar directamente en la farmacia.
• Movilidad: seguimientos a pacientes crónicos mediante Internet y sin necesidad de desplazamientos.
• Telemedicina: Administración de servicios a distancia sin necesidad de desplazamientos. "Tele-Health".
• Picture Archiving Communication System (PACs): almacenaje de todos los resultados de prueba.

Algunos conceptos nuevos:

• E-Health: Provisión de cuidados de salud mediante tecnologías de la comunicación e Información.
• M-Health: E-Health a través del móvil.
• S-Health: A través de smartphones.
• U-Health: A través de cualquier tecnología, en cualquier momento: conjunto de móvil con otros instrumentos como dispositivos, sensores, etc.

3. El uso de la "Salud móvil"

Alrededor del 93% de la población ha usado algún dispositivo móvil para acceder a Internet fuera de la vivienda. Muchos accedieron mediante móvil (la mayoría), el ordenador portátil y la tablet.

Las actividades que más se siguen son la búsqueda de información de bienes, revisión de correo electrónico y visualización de vídeos.

Por otra parte, las apps (aplicaciones móviles) también han adquirido una importante relevancia en los últimos tiempos. Pueden usarse en diferentes dispositivos electrónicos, y existen algunas destinadas a la salud (ejercicio, ciclo menstrual, seguimiento de ciertas enfermedades, etc.). 

Gracias a esto,  hemos conseguido transformar la asistencia sanitaria, facilitando a los pacientes el control de sus enfermedades o seguimientos, permitiendo una mayor implicación por parte del paciente, mejorando gestiones de enfermedades crónicas, proporcionando retroalimentaciones individualizadas y mejorando la relación entre los profesionales sanitarios y los pacientes.

4. Conceptos de red de información sanitaria.

Es la red de información del ámbito sanitario y sus organizaciones que gestiona ese ámbito sanitario, por ejemplo, la sanidad pública (SAS y consejería de salud).

Está formada por:

• Infraestructuras de comunicación: fibra óptica, circuito, sistema de transmisión, etc..
• Hardware: ordenadores, routers, etc.
• Software: Gestión de bases de datos, análisis de imágenes, etc.
• Datos: nómina, financieros, historia clínica de pacientes, etc.
• Seguridad: autentificación, seguridad de red, etc.
• Aplicaciones: correo electrónico, enlace de red, citaciones, etc.
• Interfaz y usuario:.
• Intranet: comunicación entre todos los ámbitos, radiología con urgencias, etc.
• Extranet: red externa comunicante entre todos los servicios del centro sanitario.

5.Aplicación de las tecnologías de los centros asistenciales.

Aumenta la calidad, comodidad y flexibilidad para prestar asistencia y facilitar la comunicación. Conexión entre nivel asistencial primario, especializado y domiciliario.

Estas tres aplicaciones están mejorando la gestión de los pacientes:

• Tarjeta sanitaria electrónica.
• Historia clínica electrónica.
• Hospital digital, gracias al sistema informático DIRAYA.

6. Aplicación de las TICs en la gestión de emergencias.

• Se favorece la rapidez de actuación.
• Fácil accesibilidad a información actualizada.
• Rápida información detallada de los sucesos.
• De camino al hospital se obtienen todos los datos necesarios.

7. Aplicación de las TICs en la promoción de la salud y prevención de enfermedades.

• Herramientas 2.0: imprescindibles en la diseminación de conocimientos sobre salud. Se usa en programas de salud y EpS.
• Blogs, vídeos y diferentes páginas informativas sobre enfermedades, recomendaciones de salud, apoyo psicosocial, etc.

A continuación, se facilita un vídeo bastante corto sobre la importancia de las TICs en el ámbito de la salud.

Resumen Tema 13: Pruebas paramétricas más utilizadas en enfermería. La prueba T-Student para datos apareados. Anova.

 

1. Análisis bivariado. Variable cualitativa y cuantitativa.

Muy útil para saber visualizar si diferentes factores de un tipo de variable cualitativa presentan valores medios.

2. Comparación de medias: casos.

• Media de una variable respecto a un valor de interés. Ej.: Es diferente el valor medio de colesterol de un grupo de sujetos 299 mg/dl.
• Media de dos muestras apareadas o dependientes: los valores que adquieren están relacionados. Ej.: ¿Es diferente la agregación plaquetaria de un grupo de individuos antes y después de tomar un nuevo antiagregante?
• Media de dos muestras desapareadas o independientes: Los valores que adquieren no están relacionados entre sí.  Ej.: ¿Es diferente el peso medio de chicos y chicas de esta clase?

3. Test a aplicar.

Dependiendo de ante cuántas o de qué tipo de muestras nos encontremos:

• Paramétricos
• T de Student (una o dos muestras).
• ANOVA (más de dos muestras).
• No paramétricos
• Prueba U de Mann-Whitney (muestras independientes).
• Test de Wilconxon (muestras apareadas).
• Test Kruskal-Wallis (más de dos muestras).

4. Test de Student como test paramétrico.

• Criterios de parametricidad:
• Normalidad.
• Igualdad de varianzas: Test Levene.
• N muestral > 30.

A continuación se facilita un vídeo en el que se expone un caso en el que se usaría el método T Student y su resolución:

5. ANOVA: Analysis Of Variation.

Situación básica de ANOVA.

• 2 dos variables: una categórica y una cuantitativa.
• ¿Las variables cuantitativas dependen de en qué grupo (dado por la variable categórica) está el individuo?
• Si la variable categórica tiene dos valores: 2-sample t-test.
• ANOVA permite para 3 o más grupos. 

Investigación informal.

• Investigación gráfica
• Cajas de lado a lado.
• Múltiples histogramas
• Para que las diferencias entre los grupos sean significantes dependen de:
• Las diferencias en el significado
• Las desviaciones estándares en cada grupo
• Los tamaños de muestra.

ANOVA determina el valor de P del F estadístico.

Diagramas de cajas lado a lado.

El siguiente vídeo muestra algunos ejemplos sobre cómo se realiza un diagrama de cajas.

¿Qué hace ANOVA?

• H0: Significado de todos los grupos =.
• Ha: No todos los significados son =.

Suposiciones de ANOVA.

Cada grupo es aproximadamente normal.

Las desviaciones estándares de cada grupo son aproximadamente iguales. Regla de oro: la relación de

mayor a menor, la desviación estándar de la muestra debe ser inferior a 2:1.

6. Pruebas de normalidad.

Se usa Kolmogorov (n>50) o Shapiro (n<50). Para ello:

7. Comprobación de la desviación estándar.

Se debe comparar que la desviación estándar mayor y menor cumplan la regla de oro de la que hablábamos antes.

8. Notaciones para ANOVA.

• n: Número de individuos todos juntos.
• i: número de grupos.
• Media aritmética: significado para todo el conjunto de datos.

El grupo i tiene:

• ni = # of individuals in group i
• xij = value for individual j in group i
• I : significado para el grupo i.
• si = standard deviation for group i.

9. Cómo funciona ANOVA (fuera de línea).

Mide dos fuentes de variación en los datos y compara sus medidas relativas. Miramos la variación entre grupos y dentro de los grupos.

10. ¿Cómo están estas computaciones hechas?

Este vídeo explica cómo funciona ANOVA y muestra una representación:

11. ¿Cómo de grande es F?

F = (variación entre los grupos)/(variación dentro de los grupos). A mayor F, mayor diferencia entre los grupos. 

Para obtener el valor P, comparamos con F:

• 1-1: grados de libertad en el numerador.
• n-1: grados de libertad en el denominador.

Resumen Tema 12: Concordancia y correlación

1. Relaciones entre variables y regresión

La ley de regresión universal explica los rasgos de una variable a partir de otra de la cual deriva. Por ejemplo, el estudio realizado por Pearson estudió la altura de las diferentes generaciones, concretando que aunque ciertas características de los hijos (en este caso la altura) se comparten y se parecen, suele ser en menor medida, y al final los resultados tienden a volver a la media. De padres muy altos, por tanto, seguramente tendríamos hijos altos, aunque no tanto.

2. Estudio conjunto de dos variables

• Filas: datos de los individuos.
• Columnas: Valores de una variable.

Los individuos no hace falta que estén ordenados. Podemos representar esto mediante diagramas, como el de dispersión. 

La recta, cuya ecuación es y=ax+b, indica la media, mientras más cercanos a la media estén los puntos, mayor relación existirá, y al contrario si están más separados, como en este caso:

Relación directa e inversa

A continuación se muestra un vídeo explicativo sobre cómo representar e interpretar los diagramas de dispersión.

3. Regresión lineal simple: correlación y determinación

En este caso estudiamos la asociación lineal entre dos variables cuantitativas.

La ecuación de la recta, como dijimos antes, es y=ax+b, indicando "a" la pendiente (más negativo=más decreciente y viceversa), y siendo "b" el punto de corte con el eje de coordenadas. 

Gracias a la pendiente sabemos cómo varía un variable en función de otra y gracias al punto de intersección con el eje de coordenadas sabemos el valor de la variable dependiente cuando la otra variable de la que depende es 0.

Este método es probabilístico. Existen dos coeficientes de correlación: Pearson (paramétrica) y Spearman (no paramétrica). Nos centraremos en Pearson.

4. Análisis de correlación

Estos vídeos ayudarán a analizar y comprender una correlación. En el primero se explica de dónde viene la fórmula del coeficiente de correlación de Pearson y en el segundo se mostrará un ejercicio como ejemplo.

Ver 1º:

Ver 2º:

Coeficiente de correlación y determinación

A continuación se facilita un vídeo explicativo para evitar confusiones y explicar el coeficiente de determinación y correlación.

Resumen Tema 11: Pruebas no paramétricas más utilizadas en enfermería.

1. Chi cuadrado.

Se usa para hacer análisis bivariados. Ambas variables deben ser cualitativas.

• Para comparar dos variables cualitativas.
• Razonamiento a seguir: se supone que la hipótesis nula es cierta y se estudia la probabilidad de que siendo iguales los dos grupos a comparar se obtengan resultados como los obtenidos o de haber encontrado diferencias más grandes.

Para ello se usan las tablas de contingencia. Ejemplo:

En enfermería, estudiaríamos casos relacionados con la salud.

Qué recordar:

• La frecuencia observada es la que recogen los datos.
• La frecuencia esperad es la que observaríamos si no hubiera relación.
• Los grados de libertad pueden variar libremente dando un determinado resultado.

Fórmula:

Para obtener los valores esperados:

2. Oods ratio.

Es necesario para interpretar la hipótesis de chi-cuadrado correctamente. Sirve ara calcular la magnitud de asociación.

Resumen Tema 10: Estimación y/o significación estadística.

1. Significación estadística.

• Otra forma de hacer inferencia.
• Permite contrastar hipótesis y relacionarlo con el método más científico.
• Se parte de la hipótesis nula frente a la hipótesis alternativas.
• Permite calcular el nivel de significación, si es alta se puede rechazar la hipótesis nula y viceversa.
• Permite cuantificar el error.

2. Hipótesis estadística.

Creencia sobre los parámetros de una o más poblaciones (no muestras). Pretenden comprobar si las diferencias en la muestra pueden ser omitidas y generalizar en la población.

• Hipótesis nula: Contempla la no diferencia entre los parámetros que se comparan.
• Hipótesis alternativa: Contempla la diferencia entre los parámetros que se comparan.

Cómo contrastar hipótesis:

Tipos de errores.

3. Método de contraste de hipótesis.

1. Expresar el interrogante de la investigación con hipótesis estadística (nula o alternativa).
2. Decidir prueba estadística adecuada según las características de la población y el tipo de variables de la hipótesis. Para ello:
• Si la población sigue una distribución normal, se usan métodos paramétricos:
• T-student.
• Anova.
• Fisher.
• Pearson.
• Si lapoblación no sigue una distribución normal, se usan métodos no paramétricos:
• U-Mann Whitney.
• K-W.
• Tablas de contigencia.

Tipos de análisis estadísticos según el tipo de variables implicadas en el estudio

Resumen Tema 9: Introducción a la inferencia estadística. Intervalos de confianza y contraste de hipótesis.

1. Inferencia estadística.

Procedimientos estadísticos que permiten pasar de la muestra a la población. Hay 2 formas de inferencia estadística:

• Estimación del valor en la población (parámetro) a partir de un valor de la muestra (estimador).
• Contraste de hipótesis a partir de valores de la muestra.

2. Estimaciones.

A través de la muestra se obtiene información acerca de toda la información. Pueden realizarse las siguientes estimaciones:

• Estimación puntual: El valor estadístico muestral se considera una estimación del parámetro poblacional.
• Estimación por intervalos: No es preciso pero a veces es más exacto. Se calculan dos parámetros entre los que se encuentra el parámetro poblacional. Mientras menor sea el intervalo, menor será el error.

3. Error estándar.

Es la desviación típica. Mientras más pequeño sea el error, más fiable será el valor de la muestra.

Cálculo:

• Para media: 
  
• Para una proporción:

4. Teorema central del límite.

Si sigue distribución normal, entonces:

5. Intervalos de confianza.

Sirve para conocer el parámetro de una población midiendo el error aleatorio. Son dos números entre los que se asegura que se encuentra el valor.

Cálculo:

6. Contraste de hipótesis.

Sirve para controlar los errores aleatorios y cuantificarlos. Para ello:

1. Se establece una hipótesis acerca del valor a priori.
2. Se recogen los datos.
3. Se comparan las diferencias entre la hipótesis y los datos obtenidos.

Errores de hipótesis:

• Se puede aceptar o rechazar la hipótesis nula con la misma muestra.
• El error α es la probabilidad de equivocarnos al rechazar la hipótesis nula.
• El error α más pequeño al que podemos rechazar H0 es el error p.
• Se suele rechazar H0 para un nivel α máximo del 5%.

Resumen Tema 8: Teoría de muestras.

1. Estimación e inferencia estadística.

• Técnicas de muestreo = conjunto de procedimientos para elegir una muestra que reflejen las características de la población.
• Hay que asumir cierto error.
• Si la muestra se elige al azar, el error puede calcularse, y entonces se llama "error aleatorio".
• En las muestras que no se elige al azar no se puede calcular el error.

Proceso de inferencia estadística:

Se quiere medir un parámetro en la población, se realiza una preselección de sujetos (preferiblemente de forma aleatoria) y así obtengo a muestra para realizar la interferencia.

2. Procedimiento muestral.

Al escoger al grupo pequeño de la población (muestra) se debe tener un grado de probabilidad de que el grupo posea las características de la población que estamos estudiando. La muestra debe reflejar lo más posible a realidad.

3. Tipos de muestreo.

• No probabilísticos: no azar, hay sesgos.
• Por conveniencia: El investigador decide los elementos que integrarán la muestra considerando las características "típicas" de la población que quiere conocer.
• Por cuotas: Selecciona la muestra considerando algunas variables como el sexo, la raza o la religión.
• Accidental: Se utilizan las personas disponibles en un momento dado. Es la más eficiente.
• Probabilísticos: azar, se puede dimensionar el error.
• Por conglomerados: cuando la población de estudio es geográficamente amplia. No se conoce la distribución de la variable, no es tan fiable. No se han obtenido datos de todas las unidades que se quieren estudiar.
• Estratificados: Se divide a la población en subgrupos debido a la variabilidad de las características de las personas.
• Aleatorios sistemáticos: cada ud. tiene la misma probabilidad de participar. Se sigue el mismo criterio para seleccionar (por ejemplo, selecciono personas al azar de cinco en cinco).
• Aleatorios simples: cada ud. tiene probabilidad equitativa de ser incluida en la muestra. problema si la población es muy grande.

4. Tamaño de la muestra.

Depende de:

• Error aleatorio.
• Mínima diferencia entre los grupos de comparación que se considera importante.
• Variabilidad de la variable.
• Tamaño de la población.

Si quiero calcular tamaño de una muestra para estimar una proporción:

Resumen Tema 7: Teoría de la probabilidad.

1. Probabilidad.

Es qué tan posible es que ocurra un evento determinado. Se calcula cuando no se está seguro de que ocurra algo, o para averiguar que es lo que probablemente ocurrirá.

• Probabilidad subjetiva o personalística: Mide la confianza del individuo sobre la certeza de una proposición determinada.
• Probabilidad objetiva:
• Clásica o "a priori": Un evento puede ocurrir de N formas, las cuales se excluyen mutuamente y son igualmente probables, y si m de esos eventos puede ocurrir de manera E, entonces: P(E) =m/N.
• Relativa o "a posteriori": Un evento se repite muchas veces, y si algún suceso resultante con la característica E ocurre m veces, la frecuencia relativa de la ocurrencia E, m/N es: 
  

2. Eventos o sucesos.

• Conjunto de todos los resultados posibles = espacio muestral (S).
• Suceso o evento = subconjunto de dichos resultados.
• Evento complementario de un suceso A = elementos que no están en A y están delimitados por Ac.
• Evento unión A y B = formado por los resultados experimentales que están en A o B. 

• Evento intersección A y B: formado por los elementos que están entre A y B. Se poseen ambas características.

3. Reglas básicas: teoría de la probabilidad.

• Valores entre 0 y 1.
• Probabilidad del suceso contrario, P(Ac) = 1- P(A)
• Pobabilidad de un suceso imposible = 0.
• Si los eventos son compatibles (A y B), entonces:

• Si los eventos son incompatibles, no pueden ocurrir a la vez, por lo que:

• Probabilidad condicionada de un suceso A a otro B (Teorema de Bayes)

4. Distribución de probabilidad en variables discretas: binomial y Poisson.

• Distribución binomial:
• Cuando son situaciones donde solo existen dos opciones.
• El resultado obtenido siempre es independiente a los resultados obtenidos anteriormente.
• Las probabilidades son constantes.
• P(A) = 1-p = q.
• p = probabilidad de ocurrencia.
• q= probabilidad de no ocurrencia.
• X = número de sucesos favorables.
• N = número total de ensayos.
• Factorial de 0 = 1.
• Distribución de Poisson: Uso para variables discretas y casos raros.

5. Distribuciones normales.

En la campana de Gauss se observa: media coincide con la moda en punto más alto y mediana. Si se le suma o se le resta el valor de una desviación típica a la media de cualquier serie estadística que sigue una distribución normal, el valor de esa serie se va a encontrar en el 68,26%.

Tipificación de valores en una normal.

Se puede realizar si trabajamos con variables continuas que siguen distribución normal (más de 100 uds). La tipificación nos permite saber si otro valor responde o no a esa distribución de frecuencia.

Resumen Tema 6: Representación gráfica de la infromación.

1. Representaciones gráficas.

Forma rápida de comunicar información en forma de imagen (histograma, sectores, etc.), además de complementar un análisis estadístico sin reemplazar las medidas estadísticas a calcular. Normas a seguir:

- Claridad para visualizar.

- Claridad en la descripción para la interpretación.

- Representación gráfica de las conclusiones del estudio.

- No sobrecargarlos.

2. Representaciones gráficas más empleadas.

• Variables cualitativas:
• Gráfico de sectores: dicotómicas o policotómicas.
• Gráfico de barras: solo para policotómicas.
• Pictogramas: policotómicas.
• Variables cuantitativas:
• Gráfico de barras: solo si la variable es discreta y tiene un bajo rango de valores.
• Histogramas: para variables continuas.
• Polígonos de frecuencia: para variables continuas.
• Gráficos de tronco y hoja: para variables continuas.
• Datos bidimensionales y multidimensionales:
• Se pueden mezclar variables cuantitativas y cualitativas.
• Tendencias temporales. 
• Nubes de punto. Solo para mezclar dos continuas.
• Otros.

3. Variables cualitativas (dicotómicas o de pocas categorías).

• Gráfico de sectores:
• Área de cada sector proporcional a la frecuencia (absoluta o relativa) de las categorías de la vaiable.
• No se pueden usar variables ordinales.
• No debe usarse para más de tres o cuatro categorías.
• Solo muestra una variable.

• Cuidado con las variables policotómicas y ordinales.
• Diagrama de barras:
• Se muestran todas las categorías de una variable (frecuencias absolutas o relativas) fácilmente.
• Cada barra = una categoría. Su altura = frecuencia (absoluta/relativa).
• Barras separadas.
• Eje Y empieza en 0.

• Si se quieren comparar dos gráficas, las frecuencias deben ser RELATIVAS. Cuidado si hay muchas categorías, en ese caso es mejor el histograma.
• Pictograma: No aporta información, sino que ayuda a visualizar.

4. Variables cuantitativas.

• Histograma.
• Rectángulos contiguos.
• Variable continua con datos agrupados en intervalos.
• Base de cada rectángulo = amplitud de cada intervalo. Altura determinada por frecuencia.

• Cuidado con confundir con diagrama de barras o con no tener en cuenta las amplitudes de los intervalos.
• Gráfico de troncos (o tallo) y hojas: híbrido entre tabla de frecuencia e histograma. Muestra distribución y valores de la variable.

• Gráficos para datos bidimensionales: No se puede representar más de una variable en el mismo gráfico.
• Gráficos de tendencias temporales:

• Diagramas de dispersión (nube de puntos o (scatter plot): Para representar dos variables continuas, donde el eje X = variable independiente y el eje Y= variable dependiente. La imagen nos muestra una posible correlación entre las variables.

• Diagrama de estrellas: para representar variables cuantitativas y comparar entre diferentes unidades. Cada variable =vértice del polígono.

Resumen Tema 5: Estadísticos univariables: medidas resumen para variables cuantitativas.

1. Resumen numérico de una serie estadística.

3 tipos de medidas estadísticas:

• Medidas de tendencia central: Muestran una idea general acerca del resto de valores.
• Medidas de dispersión o variabilidad: Información acerca de la heterogeneidad u homogeneidad de nuestras observaciones.
• Medidas de posición: se ordena un conjunto de datos de menor a mayor.

2. Medidas de tendencia central.

• Media aritmética o media (x): En poblaciones se representa con μ.
• La calculamos en variables cuantitativas. Fórmula:

• Mediana: observación de forma que 50% = datos menores, 50% = datos mayores.
• Si el nº observaciones es impar, valor de observación = (n/2)+1.
• Si el nº de observaciones es par, hay que hacer media entre (n/2) y (n/2)+1.

• Moda: valor que más veces se repite.Si hay dos = bimodal, si hay más de dos = multimodal. Sirve para variables cuantitativas y cualitativas.

3. Medidas de posición

Medidas que permiten ubicar el valor en una posición. Para variables cuantitativas. De menor a mayor:

• Cuantil: medida más general. Se representan mediante Q1, Q2, Q3... Los más usuales:
• Percentil: divide la muestra en 100 partes.
• Decil: Divide la muestra en 10 partes.
• Cuartil: Divide la muestra en 4 partes.

4. Medidas de dispersión.

También llamadas de variabilidad.

• Rango o recorrido: Diferencia entre valor mayor y menos.

• Desviación media: Media aritmética de las distancias de cada observación con respecto a la media de la muestra.

• Desviación típica o estándar: Cuantifica el error que cometemos si solo se usa la media. No puede ser superior a la media.

• Varianza: Desviación típica al cuadrado. 
• Recorrido intercuartílico: diferencia entre tercer y primer cuartil.
• Coeficiente de variación: Para comparar heterogeneidad de dos series numéricas con independencia de las unidades medidas. Valores entre 0 y 1. C.v. = s/media

5. Resumen numérico de una variable continua.

Estudio multicéntrico.

6. Distribuciones normales.

También llamada de Gauss. La función de densidad tiene forma de campana, y es simétrica.

Asimetrías y curtosis.

• Asimétrica hacia la izquierda (o negativa)= grado de asimetría < 0.
• Simétrica = grado de asimetría = 0.
• Asimétrica hacia la derecha (o positiva) > 0.

Curtosis o apuntamiento.

Para medir el grado de concentración de valores en torno a su media.

• Leptocúrtica = grado de curtosis > 0. Elevado grado de concentración en torno a los valores centrales.
• Mesocúrtica = grado de curtosis = 0. Concentración media en torno a los valores centrales.
• Platicúrtica = grado de curtosis < 0. Reducido grado de concentración en torno a los valores centrales.

Resumen Tema 4: Introducción a la estadística descriptiva.

1. Estadística descriptiva.

• Para describir, resumir y organizar datos. 
• Más común en medios de comunicación. 
• No pretende sacar conclusiones generales. 
• Usa métodos numéricos y gráficos para presentar la información obtenida.
• Explora las relaciones entre las variables (comparación de grupos).
• Preliminar antes de la inferencia.

Variables.

Forma más básica de presentación de datos = tabla de frecuencias.Estas se distribuyen en columnas y filas. Su uso facilita la comprensión de los datos y favorece la visión global del conjunto. Indican frecuencias absolutas (número absoluto, información insuficiente) y relativas (información proporcional).

Variables continuas: tablas de frecuencia.

Son los datos desagrupados a estudiar. 

• N = número de datos que se van a estudiar.
• Frecuencia absoluta (fi) = número de individuos incluidos en un dato común o intervalo.
• Frecuencias acumuladas  = número de individuos menores o iguales que la modalidad o el intervalo que estamos estudiando.
• Frecuencia absoluta acumulada (Fi) = referido a los datos de la frecuencia absoluta.
• Frecuencia relativa acumulada (Hi) = referido a los datos de la frecuencia relativa.
• Frecuencia relativa (hi) = proporción de individuos incluidos en un dato común o intervalo.

Ejemplo:

Indicadores.

Es la medida de frecuencia de un determinado suceso en una población expresado como un número. Puede ser una proporción, una tasa, razón u oods. Están formados por numerador y denominador. Por ello no usamos la frecuencia absoluta como indicador, pues no da información suficiente al no tener numerador y denominador.

• Proporciones: medida resumen para variables cualitativas. Comparación (en fracción/división). 
• Numerador siempre incluido en denominador.
• Valores reales entre 0 y 1.
• Se suele expresar mediante porcentaje.
• Se puede multiplicar por 1000, 10.000...
• Tasas (rate): medida que expresa el riesgo de ocurrencia del evento estudiado. 
• Proporción que relaciona espacio y tiempo = comparación en forma de fracción entre el número de veces que ocurre un fenómeno y la población en la que puede ocurrir dicho fenómeno.
• El resultado de la fracción suele estar entre 0 y 1. 
• Podemos multiplicar por múltiplos de 10.

Medidas más empleadas en estadísticas sanitarias

• Prevalencia: la situación de la población en un punto en el tiempo (población que tiene la enfermedad en un momento dado). 
• Prevalencia = (nº de individuos con la enfermedad en un tiempo específico)/(nº de individuos en la población en un punto en el tiempo).
• Incidencia: lo que estás pasando en un periodo de tiempo (frecuencia de nuevos casos en un periodo de tiempo). Podemos medir la incidencia mediante:
• Incidencia acumulada = (nº de nuevos casos detectados durante el seguimiento que desarrollan la enfermedad)/(nº de sujetos libres de enfermedad al comienzo del seguimiento). Mide el riesgo de padecer la enfermedad.
• Densidad de incidencia = (nuevos casos)/(personas-tiempo a riesgo).
• Es una tasa instantánea (valores mayores que 1).
• Expresa velocidad.
• Persona-tiempo: suma de tiempos que los individuos están a riesgo de padecer la enfermedad. Las unidades a utilizar dependen del investigador.

2. Estadística inferencial.

Se saca muestra a partir de población. Más frecuente en investigaciones científicas. Se apoya en el cálculo y la probabilidad, efectuando estimaciones, decisiones, predicciones y generalizaciones.

3. Razones o "ratios".

• Medida de resumen para variables cualitativas.
• Numerador y denominador distintos, uno no incluye al otro.
• Ej.: tengo 60 mujeres y 10 hombres. Para saber la razón de mujeres sobre hombres = nº mujeres/nº hombres.

7. Oods o ventaja.

• Cociente entre proporción o probabilidad de ocurrencia de un evento y la proporción o probabilidad de no ocurrencia.
• Forma de cálculo: O = p/(1-p).
• No existe término exacto para definirlo.
• Valores entre 0 e infinito.

Medidas de asociación: relaciones entre proporción, ratios y oods.

• Para medir fuerzas de asociación.
• Se usan unos u otros dependiendo del estudio.
• Tres más importantes:
• Razón de prevalencias: razón entre dos prevalencias.
• Riesgo relativo o razón de riesgo: ratio entre dos incidencias acumuladas.
• Oods ratio: estudios de casos y controles.

Resumen Tema 3: De los conceptos a las variables. Población, muestra, parámetros y estadísticos. Variables y escalas de medidas.

1. Estadística.

Conocimiento que se obtiene en forma de números, variando de un individuo a otro.

2. Procedimiento muestral.

Método que consiste en escoger un grupo pequeño de una población lo suficientemente significativa como para representar a la población completa. La selección debe ser aleatoria.

Proceso de la inferencia estadística.

• Tamaño de la población = N.
• Parámetro = lo que queremos medir. Se expresan con letras griegas.
• μ = media.
• σ = desviación típica.
• π = proporción.
• Muestra = n.
• Valor estimador = valor aproximado al parámetro. Para ello hacemos inferencia.

Parámetros y estadísticos.

• Parámetros: Cantidad numérica calculada sobre una población cuyo tamaño se expresa con N.
• Estadísticos: Cantidad numérica calculada sobre una muestra extraída de la población, cuyo valor se expresa con n.

Este vídeo explica las diferencias entre muestra y población mediante ejemplos:

3. Conceptos de la teoría de medición.

• Mediciones directas: Exactitud. Ej.: presión arterial, peso, talla, etc. Las enfermeras recogen medidas como edad, género, origen étnico, estado civil o nivel de ingresos.
• Mediciones indirectas: Ideas abstractas. Ej.: grado de dolor, grado de cansancio del cuidador, etc. Las enfermeras recogen medidas como nivel de estrés, cuidado, ansiedad, dolor (mediante escalas) o afrontamiento. No es muy exacto.

Medición de signos y síntomas.

Diferentes método de medición según la naturaleza de la variable.

4. Escalas de medida.

• Escala nominal: nivel inferior de medida. Números usados con nombres. Cada número es una categoría. Solo puede comprobar la igualdad o diferencia de categorías o variables.
• Escala ordinal: A dos o más modalidades de una variable. Se establece si son iguales o diferentes. Las distancias o intervalos no representan distancias equivalentes.
• Escala de intervalo: Características de las anteriores. Las distancias o intervalos representan distancias equivalentes. No puede sacar razones o proporciones. Escala cuantitativa, se puede aplicar as estadísticas.
• Escala de razón: Igual que la escala de intervalo. Nivel más alto de medición, no admite números negativos. Distancia equivalente entre intervalos, posee el 0.

5. Tipos de variables.

Se deben tener en cuenta dos criterios: exhaustividad y exclusividad.

• Cualitativas: Propiedades que no pueden ser medidas.
• Nominales: Dicotómicas (dos niveles) o policotómicas (más de dos niveles).
• Ordinales: establecen un orden. Escalas.
• Cuantitativas: Pueden ser medidas.
• Discretas: Número finito. No fracciones.
• Continuas: cualquier valor dentro de un rango, se admiten fracciones.

Operativización de las variables.

Proceso que transforma una variable subjetiva en una susceptible de medición. Las variables principales se descomponen en otras más específicas llamadas dimensiones. Varias dimensiones:

• Accesibilidad geográfica.
• Accesibilidad económica.
• Accesibilidad cultural.

Resumen Tema 2: El método científico y sus perspectivas.

Investigamos para: obtener información y acercarnos a las diferentes realidades mediante distintos enfoques, métodos y técnicas.

1. Proceso deductivo: métodos estadísticos (cuantitativo).

Estudia de lo particular a lo general mediante procesos aleatorios, recogiendo datos, haciendo estimaciones y contrastando hipótesis. De esta forma se pueden deducir parámetros, leyes o confirmar teorías.

Esta recogida de datos se hace mediante cuestionarios (preguntas cerradas generalmente) y mediciones de variables. Los cuestionarios y preguntas no proporcionan resultados 100% reales, puesto que algunos mienten o no contestan de la forma adecuada.

2. Proceso inductivo: métodos cualitativos.

Se parte de lo general para estudiar lo particular, los llamados "informantes clave", con cierta representatividad sobre el grupo general. No se usan los números.

Atributos de los paradigmas cualitativo y cuantitativo

• Paradigma cualitativo

1. Métodos cualitativos.
2. Fenomenologismo y comprensión.
3. Observación naturalista y sin control.
4. Subjetivo.
5. Próximo a los datos.
6. Fundamento en la realidad.
7. Orientado al proceso.
8. Válido.
9. No generalizable.
10. Holístico.
11. Asume realidad dinámica.

• Paradigma cuantitativo

1. Métodos cuantitativos.
2. Positivismo lógico.
3. Medición penetrante y controlada.
4. Objetivo.
5. Al margen de los datos.
6. Fundamentado no en la realidad.
7. Orientado al resultado.
8. Fiable.
9. Generalizable.
10. Particularista.
11. Asume una realidad estable.

A continuación se facilita un vídeo explicativo sobre la diferencia entre un razonamiento inductivo y deductivo.

3. Fases del proceso de investigación 

• Etapa conceptual: Se define qué se quiere investigar y para qué.
• Etapa empírica: Cómo investigarlo (datos a recoger, población, etc.).
• Etapa interpretativa: Interpretación de resultados, cuál es su significado.

4. Etapa conceptual de la metodología de la investigación

1. Observación de hechos
2. Identificación y formulación del problema.
3. Revisión bibliográfica (antecedentes).
4. Marco teórico o marco de referencia conceptual (base teórica del problema).
5. Definición del problema de investigación.
6. Definición de objetivos/formulación de la hipótesis (estudios cuantitativos analíticos).
7. Definición operacional de términos y variables.
8. Importancia del estudio y limitaciones.

Definición y formulación de objetivos

• Definir a dónde queremos llegar con la investigación.
• No confundir objetivos de investigación con objetivos de la práctica profesional.
• Características de los objetivos: pertinentes, concretos, realistas y mensurables.

Hipótesis

• Enunciado de las expectativas de la investigación (mediante dos o más variables).
• Las investigaciones cualitativas no llevan hipótesis.
• Enlaza las variables dependiente e independiente.
• Definición previa y clara de las variables.
• "Hipótesis nula": no tiene relación entre ambas variables.

5. Etapa empírica proceso de investigación.

• Etapa más práctica.
• Material, métodos y obtención de resultados.
• Define plan de investigación.
• Asegura control o comprobación y validez interna y externa.

Conformada por:

• Planificación de la investigación (material y métodos):

1. Diseño metodológico.
2. Población del estudio.
3. Muestreo o selección de participantes.
4. Variables.
5. Definición del proceso de recogida de datos.
6. Registro y procesamiento.

• Trabajo de campo: Recogida de datos.
• Análisis de los datos.

Tipos de diseño cuantitativos en función del objetivo de las investigaciones

• Analíticos: analiza la relación entre dos variables.
• Los estudios de casos y controles: búsqueda de la causa en el pasado. Se parte del efecto.
• Seguimiento: se parte del efecto para buscar la causa.
• Experimentales: el investigador manipula y observa la variable independiente.
• Aleatorios controlados: elección al azar de participantes.
• Cuasiexperimentos.

Métodos cualitativos de investigación

Descriptivos:

• Documentales, históricos, iconográficos, fotográficos, etc.
• Etnográficos: investigación participativa.
• Fenomenológico: biográficos.

6. Etapa interpretativa del proceso de investigación

• Convalidación de los métodos empleados.
• Convalidación de los resultados.
• Describir fortalezas y debilidades del estudio.
• Relación de los hallazgos con los objetivos e hipótesis.
• Relación de los hallazgos con los hallazgos de otros autores.
• Aspectos novedosos y relevantes.
• Extraer conclusiones.

7. Artículo científico (original o primario)

Estructura

• Preliminares
• Título
• Autor
• Institución
• Resumen
• Cuerpo
• Introducción
• Metodología
• Resultados
• Discusión
• Conclusiones
• Finales
• Agradecimientos
• Referencias
• Apéndices

8. Errores en los estudios cuantitativos

• Aleatorios: debidos al azar. Cuando el estudio se realiza sobre una muestra probabilística de la población. La muestra es solo una representación, no el resultado real, por lo que el resultado puede superar o quedarse corto respecto al resultado real poblacional. Para evitar los máximos errores posibles, existen unas medidas de control:
• Primera fase: Calcular el tamaño mínimo de una muestra necesario para poder detectar cómo estadísticamente significa una diferencia.
• Segunda fase: Uso de pruebas o tests de hipótesis. Para ver si hay relación entre las variables.
• Tercera fase: cálculo de intervalos de confianza para las estimaciones obtenidas.
• Sistemáticos (sesgos): errores del investigador. Afectan a la validez interna del estudio. Existen varios tipos de sesgos:
• De selección: mal selección de la muestra.
• De clasificación o información: clasificar incorrectamente a un sujeto. Puede ser no diferencial (disminuye las diferencias realmente existentes), diferencial (exagera las diferencias realmente existentes). 
• De confusión: si se contrastan dos datos y uno de ellos no se ha estudiado.
• Para evitar los sesgos: grupo control:
• Efecto Hawthorne: sentirse observado mejora la respuesta.
• Efecto Placebo: administración de fármaco.
• Regresión de media: cuando se obtienen valores extremos en una variable la siguiente vez se tiende a la media.

9. Control de errores en los estudios estadísticos.

• En la fase de diseño.
• Rstricciones y apareamientos.
• Análisis estratificado y multivariante.

Validez interna y externa

• Interna: ausencia de sesgos para la población estudiada, replicabilidad.
• Externa: para que una medición mida aquello para lo que está destinada.

Para evaluar la validez o exactitud

• Validez de criterio: Comparación con una medida de referencia objetiva y fiable.
• Validez de concepto: Analiza la correlación de la medida con otras variables.
• Validez de contenido: Contemplar todas las dimensiones del fenómeno que se quiere medir.

Precisión y exactitud. Estrategias.

• Seleccionar las medidas más objetivas posibles.
• Estandarizar la definición de variables
• Formar y entrenar a los observadores.
• Utilizar la mejor técnica posible.
• Utilizar instrumentos automáticos.
• Obtener varias mediciones de una variable para mejorar la precisión.
• Emplear técnicas de enmascaramiento.
• Calibrar instrumentos.

10. Ética e investigación

• Respetar principios éticos en toda la investigación.
• Consentimiento informado de los participantes.
• Autorizaciones de los comités éticos de los centros.
• Uso de documentos de referencia.