Resumen Tema 5: Estadísticos univariables: medidas resumen para variables cuantitativas.

1. Resumen numérico de una serie estadística.

3 tipos de medidas estadísticas:

• Medidas de tendencia central: Muestran una idea general acerca del resto de valores.
• Medidas de dispersión o variabilidad: Información acerca de la heterogeneidad u homogeneidad de nuestras observaciones.
• Medidas de posición: se ordena un conjunto de datos de menor a mayor.

2. Medidas de tendencia central.

• Media aritmética o media (x): En poblaciones se representa con μ.
• La calculamos en variables cuantitativas. Fórmula:

• Mediana: observación de forma que 50% = datos menores, 50% = datos mayores.
• Si el nº observaciones es impar, valor de observación = (n/2)+1.
• Si el nº de observaciones es par, hay que hacer media entre (n/2) y (n/2)+1.

• Moda: valor que más veces se repite.Si hay dos = bimodal, si hay más de dos = multimodal. Sirve para variables cuantitativas y cualitativas.

3. Medidas de posición

Medidas que permiten ubicar el valor en una posición. Para variables cuantitativas. De menor a mayor:

• Cuantil: medida más general. Se representan mediante Q1, Q2, Q3... Los más usuales:
• Percentil: divide la muestra en 100 partes.
• Decil: Divide la muestra en 10 partes.
• Cuartil: Divide la muestra en 4 partes.

4. Medidas de dispersión.

También llamadas de variabilidad.

• Rango o recorrido: Diferencia entre valor mayor y menos.

• Desviación media: Media aritmética de las distancias de cada observación con respecto a la media de la muestra.

• Desviación típica o estándar: Cuantifica el error que cometemos si solo se usa la media. No puede ser superior a la media.

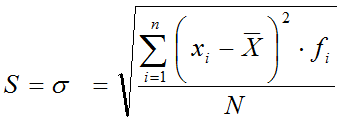
• Varianza: Desviación típica al cuadrado. 
• Recorrido intercuartílico: diferencia entre tercer y primer cuartil.
• Coeficiente de variación: Para comparar heterogeneidad de dos series numéricas con independencia de las unidades medidas. Valores entre 0 y 1. C.v. = s/media

5. Resumen numérico de una variable continua.

Estudio multicéntrico.

6. Distribuciones normales.

También llamada de Gauss. La función de densidad tiene forma de campana, y es simétrica.

Asimetrías y curtosis.

• Asimétrica hacia la izquierda (o negativa)= grado de asimetría < 0.
• Simétrica = grado de asimetría = 0.
• Asimétrica hacia la derecha (o positiva) > 0.

Curtosis o apuntamiento.

Para medir el grado de concentración de valores en torno a su media.

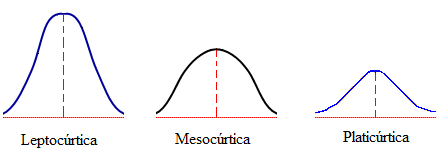
• Leptocúrtica = grado de curtosis > 0. Elevado grado de concentración en torno a los valores centrales.
• Mesocúrtica = grado de curtosis = 0. Concentración media en torno a los valores centrales.
• Platicúrtica = grado de curtosis < 0. Reducido grado de concentración en torno a los valores centrales.