Resumen Tema 7: Teoría de la probabilidad.

1. Probabilidad.

Es qué tan posible es que ocurra un evento determinado. Se calcula cuando no se está seguro de que ocurra algo, o para averiguar que es lo que probablemente ocurrirá.

• Probabilidad subjetiva o personalística: Mide la confianza del individuo sobre la certeza de una proposición determinada.
• Probabilidad objetiva:
• Clásica o "a priori": Un evento puede ocurrir de N formas, las cuales se excluyen mutuamente y son igualmente probables, y si m de esos eventos puede ocurrir de manera E, entonces: P(E) =m/N.
• Relativa o "a posteriori": Un evento se repite muchas veces, y si algún suceso resultante con la característica E ocurre m veces, la frecuencia relativa de la ocurrencia E, m/N es: 
  

2. Eventos o sucesos.

• Conjunto de todos los resultados posibles = espacio muestral (S).
• Suceso o evento = subconjunto de dichos resultados.
• Evento complementario de un suceso A = elementos que no están en A y están delimitados por Ac.
• Evento unión A y B = formado por los resultados experimentales que están en A o B. 

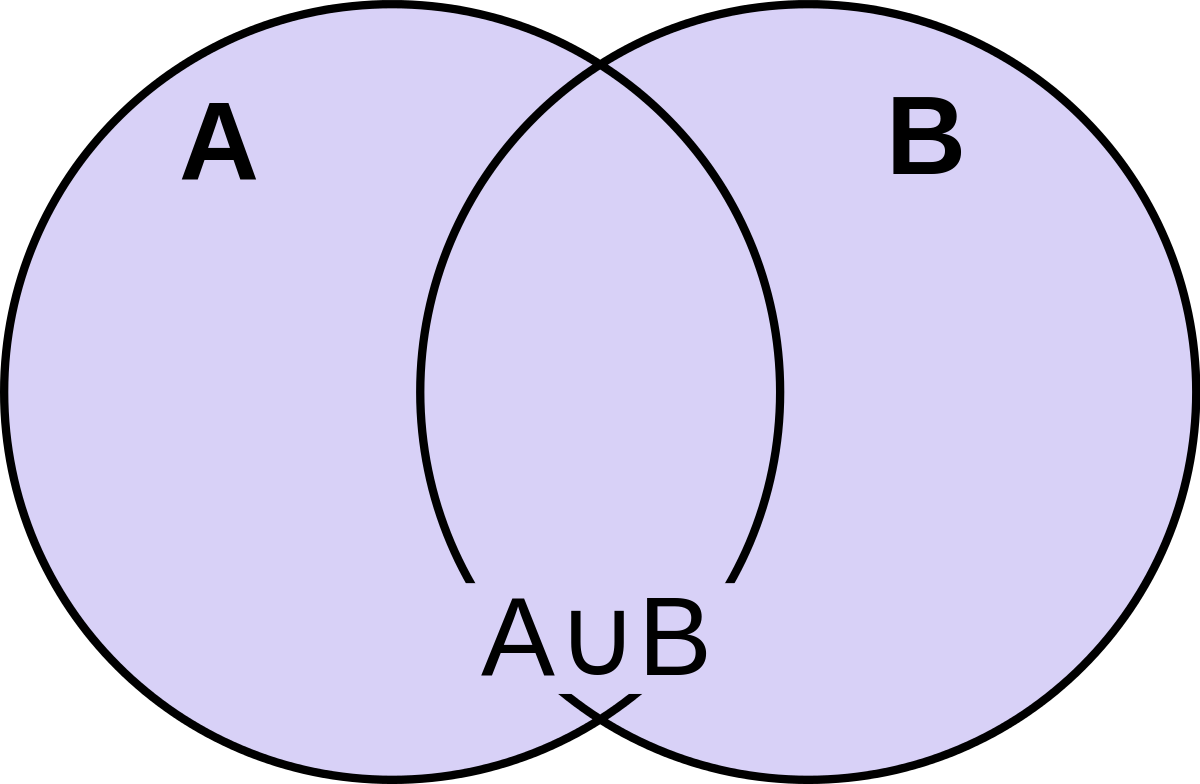
• Evento intersección A y B: formado por los elementos que están entre A y B. Se poseen ambas características.

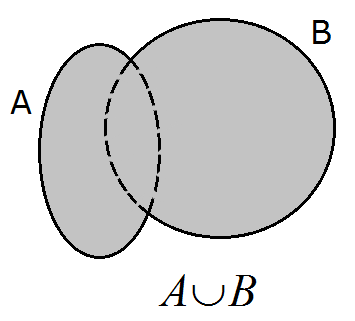
3. Reglas básicas: teoría de la probabilidad.

• Valores entre 0 y 1.
• Probabilidad del suceso contrario, P(Ac) = 1- P(A)
• Pobabilidad de un suceso imposible = 0.
• Si los eventos son compatibles (A y B), entonces:

• Si los eventos son incompatibles, no pueden ocurrir a la vez, por lo que:

• Probabilidad condicionada de un suceso A a otro B (Teorema de Bayes)

4. Distribución de probabilidad en variables discretas: binomial y Poisson.

• Distribución binomial:
• Cuando son situaciones donde solo existen dos opciones.
• El resultado obtenido siempre es independiente a los resultados obtenidos anteriormente.
• Las probabilidades son constantes.
• P(A) = 1-p = q.
• p = probabilidad de ocurrencia.
• q= probabilidad de no ocurrencia.
• X = número de sucesos favorables.
• N = número total de ensayos.
• Factorial de 0 = 1.
• Distribución de Poisson: Uso para variables discretas y casos raros.

5. Distribuciones normales.

En la campana de Gauss se observa: media coincide con la moda en punto más alto y mediana. Si se le suma o se le resta el valor de una desviación típica a la media de cualquier serie estadística que sigue una distribución normal, el valor de esa serie se va a encontrar en el 68,26%.

Tipificación de valores en una normal.

Se puede realizar si trabajamos con variables continuas que siguen distribución normal (más de 100 uds). La tipificación nos permite saber si otro valor responde o no a esa distribución de frecuencia.