Resumen Tema 11: Pruebas no paramétricas más utilizadas en enfermería.

1. Chi cuadrado.

Se usa para hacer análisis bivariados. Ambas variables deben ser cualitativas.

• Para comparar dos variables cualitativas.
• Razonamiento a seguir: se supone que la hipótesis nula es cierta y se estudia la probabilidad de que siendo iguales los dos grupos a comparar se obtengan resultados como los obtenidos o de haber encontrado diferencias más grandes.

Para ello se usan las tablas de contingencia. Ejemplo:

En enfermería, estudiaríamos casos relacionados con la salud.

Qué recordar:

• La frecuencia observada es la que recogen los datos.
• La frecuencia esperad es la que observaríamos si no hubiera relación.
• Los grados de libertad pueden variar libremente dando un determinado resultado.

Fórmula:

Para obtener los valores esperados:

2. Oods ratio.

Es necesario para interpretar la hipótesis de chi-cuadrado correctamente. Sirve ara calcular la magnitud de asociación.

Resumen Tema 10: Estimación y/o significación estadística.

1. Significación estadística.

• Otra forma de hacer inferencia.
• Permite contrastar hipótesis y relacionarlo con el método más científico.
• Se parte de la hipótesis nula frente a la hipótesis alternativas.
• Permite calcular el nivel de significación, si es alta se puede rechazar la hipótesis nula y viceversa.
• Permite cuantificar el error.

2. Hipótesis estadística.

Creencia sobre los parámetros de una o más poblaciones (no muestras). Pretenden comprobar si las diferencias en la muestra pueden ser omitidas y generalizar en la población.

• Hipótesis nula: Contempla la no diferencia entre los parámetros que se comparan.
• Hipótesis alternativa: Contempla la diferencia entre los parámetros que se comparan.

Cómo contrastar hipótesis:

Tipos de errores.

3. Método de contraste de hipótesis.

1. Expresar el interrogante de la investigación con hipótesis estadística (nula o alternativa).
2. Decidir prueba estadística adecuada según las características de la población y el tipo de variables de la hipótesis. Para ello:
• Si la población sigue una distribución normal, se usan métodos paramétricos:
• T-student.
• Anova.
• Fisher.
• Pearson.
• Si lapoblación no sigue una distribución normal, se usan métodos no paramétricos:
• U-Mann Whitney.
• K-W.
• Tablas de contigencia.

Tipos de análisis estadísticos según el tipo de variables implicadas en el estudio

Resumen Tema 9: Introducción a la inferencia estadística. Intervalos de confianza y contraste de hipótesis.

1. Inferencia estadística.

Procedimientos estadísticos que permiten pasar de la muestra a la población. Hay 2 formas de inferencia estadística:

• Estimación del valor en la población (parámetro) a partir de un valor de la muestra (estimador).
• Contraste de hipótesis a partir de valores de la muestra.

2. Estimaciones.

A través de la muestra se obtiene información acerca de toda la información. Pueden realizarse las siguientes estimaciones:

• Estimación puntual: El valor estadístico muestral se considera una estimación del parámetro poblacional.
• Estimación por intervalos: No es preciso pero a veces es más exacto. Se calculan dos parámetros entre los que se encuentra el parámetro poblacional. Mientras menor sea el intervalo, menor será el error.

3. Error estándar.

Es la desviación típica. Mientras más pequeño sea el error, más fiable será el valor de la muestra.

Cálculo:

• Para media: 
  
• Para una proporción:

4. Teorema central del límite.

Si sigue distribución normal, entonces:

5. Intervalos de confianza.

Sirve para conocer el parámetro de una población midiendo el error aleatorio. Son dos números entre los que se asegura que se encuentra el valor.

Cálculo:

6. Contraste de hipótesis.

Sirve para controlar los errores aleatorios y cuantificarlos. Para ello:

1. Se establece una hipótesis acerca del valor a priori.
2. Se recogen los datos.
3. Se comparan las diferencias entre la hipótesis y los datos obtenidos.

Errores de hipótesis:

• Se puede aceptar o rechazar la hipótesis nula con la misma muestra.
• El error α es la probabilidad de equivocarnos al rechazar la hipótesis nula.
• El error α más pequeño al que podemos rechazar H0 es el error p.
• Se suele rechazar H0 para un nivel α máximo del 5%.

Resumen Tema 8: Teoría de muestras.

1. Estimación e inferencia estadística.

• Técnicas de muestreo = conjunto de procedimientos para elegir una muestra que reflejen las características de la población.
• Hay que asumir cierto error.
• Si la muestra se elige al azar, el error puede calcularse, y entonces se llama "error aleatorio".
• En las muestras que no se elige al azar no se puede calcular el error.

Proceso de inferencia estadística:

Se quiere medir un parámetro en la población, se realiza una preselección de sujetos (preferiblemente de forma aleatoria) y así obtengo a muestra para realizar la interferencia.

2. Procedimiento muestral.

Al escoger al grupo pequeño de la población (muestra) se debe tener un grado de probabilidad de que el grupo posea las características de la población que estamos estudiando. La muestra debe reflejar lo más posible a realidad.

3. Tipos de muestreo.

• No probabilísticos: no azar, hay sesgos.
• Por conveniencia: El investigador decide los elementos que integrarán la muestra considerando las características "típicas" de la población que quiere conocer.
• Por cuotas: Selecciona la muestra considerando algunas variables como el sexo, la raza o la religión.
• Accidental: Se utilizan las personas disponibles en un momento dado. Es la más eficiente.
• Probabilísticos: azar, se puede dimensionar el error.
• Por conglomerados: cuando la población de estudio es geográficamente amplia. No se conoce la distribución de la variable, no es tan fiable. No se han obtenido datos de todas las unidades que se quieren estudiar.
• Estratificados: Se divide a la población en subgrupos debido a la variabilidad de las características de las personas.
• Aleatorios sistemáticos: cada ud. tiene la misma probabilidad de participar. Se sigue el mismo criterio para seleccionar (por ejemplo, selecciono personas al azar de cinco en cinco).
• Aleatorios simples: cada ud. tiene probabilidad equitativa de ser incluida en la muestra. problema si la población es muy grande.

4. Tamaño de la muestra.

Depende de:

• Error aleatorio.
• Mínima diferencia entre los grupos de comparación que se considera importante.
• Variabilidad de la variable.
• Tamaño de la población.

Si quiero calcular tamaño de una muestra para estimar una proporción:

Resumen Tema 7: Teoría de la probabilidad.

1. Probabilidad.

Es qué tan posible es que ocurra un evento determinado. Se calcula cuando no se está seguro de que ocurra algo, o para averiguar que es lo que probablemente ocurrirá.

• Probabilidad subjetiva o personalística: Mide la confianza del individuo sobre la certeza de una proposición determinada.
• Probabilidad objetiva:
• Clásica o "a priori": Un evento puede ocurrir de N formas, las cuales se excluyen mutuamente y son igualmente probables, y si m de esos eventos puede ocurrir de manera E, entonces: P(E) =m/N.
• Relativa o "a posteriori": Un evento se repite muchas veces, y si algún suceso resultante con la característica E ocurre m veces, la frecuencia relativa de la ocurrencia E, m/N es: 
  

2. Eventos o sucesos.

• Conjunto de todos los resultados posibles = espacio muestral (S).
• Suceso o evento = subconjunto de dichos resultados.
• Evento complementario de un suceso A = elementos que no están en A y están delimitados por Ac.
• Evento unión A y B = formado por los resultados experimentales que están en A o B. 

• Evento intersección A y B: formado por los elementos que están entre A y B. Se poseen ambas características.

3. Reglas básicas: teoría de la probabilidad.

• Valores entre 0 y 1.
• Probabilidad del suceso contrario, P(Ac) = 1- P(A)
• Pobabilidad de un suceso imposible = 0.
• Si los eventos son compatibles (A y B), entonces:

• Si los eventos son incompatibles, no pueden ocurrir a la vez, por lo que:

• Probabilidad condicionada de un suceso A a otro B (Teorema de Bayes)

4. Distribución de probabilidad en variables discretas: binomial y Poisson.

• Distribución binomial:
• Cuando son situaciones donde solo existen dos opciones.
• El resultado obtenido siempre es independiente a los resultados obtenidos anteriormente.
• Las probabilidades son constantes.
• P(A) = 1-p = q.
• p = probabilidad de ocurrencia.
• q= probabilidad de no ocurrencia.
• X = número de sucesos favorables.
• N = número total de ensayos.
• Factorial de 0 = 1.
• Distribución de Poisson: Uso para variables discretas y casos raros.

5. Distribuciones normales.

En la campana de Gauss se observa: media coincide con la moda en punto más alto y mediana. Si se le suma o se le resta el valor de una desviación típica a la media de cualquier serie estadística que sigue una distribución normal, el valor de esa serie se va a encontrar en el 68,26%.

Tipificación de valores en una normal.

Se puede realizar si trabajamos con variables continuas que siguen distribución normal (más de 100 uds). La tipificación nos permite saber si otro valor responde o no a esa distribución de frecuencia.

Resumen Tema 6: Representación gráfica de la infromación.

1. Representaciones gráficas.

Forma rápida de comunicar información en forma de imagen (histograma, sectores, etc.), además de complementar un análisis estadístico sin reemplazar las medidas estadísticas a calcular. Normas a seguir:

- Claridad para visualizar.

- Claridad en la descripción para la interpretación.

- Representación gráfica de las conclusiones del estudio.

- No sobrecargarlos.

2. Representaciones gráficas más empleadas.

• Variables cualitativas:
• Gráfico de sectores: dicotómicas o policotómicas.
• Gráfico de barras: solo para policotómicas.
• Pictogramas: policotómicas.
• Variables cuantitativas:
• Gráfico de barras: solo si la variable es discreta y tiene un bajo rango de valores.
• Histogramas: para variables continuas.
• Polígonos de frecuencia: para variables continuas.
• Gráficos de tronco y hoja: para variables continuas.
• Datos bidimensionales y multidimensionales:
• Se pueden mezclar variables cuantitativas y cualitativas.
• Tendencias temporales. 
• Nubes de punto. Solo para mezclar dos continuas.
• Otros.

3. Variables cualitativas (dicotómicas o de pocas categorías).

• Gráfico de sectores:
• Área de cada sector proporcional a la frecuencia (absoluta o relativa) de las categorías de la vaiable.
• No se pueden usar variables ordinales.
• No debe usarse para más de tres o cuatro categorías.
• Solo muestra una variable.

• Cuidado con las variables policotómicas y ordinales.
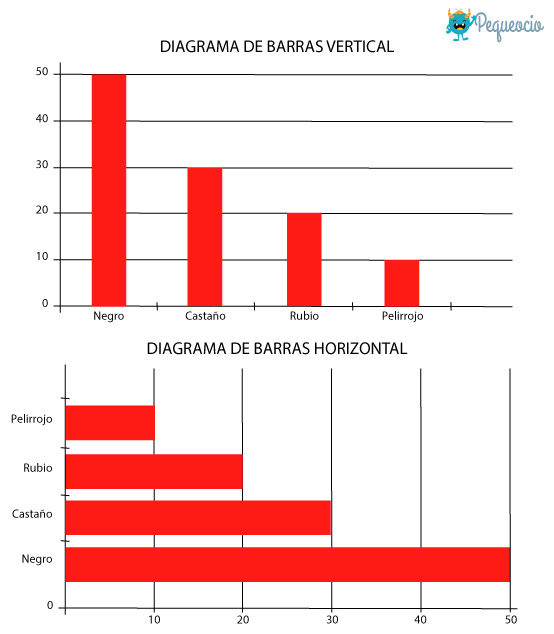
• Diagrama de barras:
• Se muestran todas las categorías de una variable (frecuencias absolutas o relativas) fácilmente.
• Cada barra = una categoría. Su altura = frecuencia (absoluta/relativa).
• Barras separadas.
• Eje Y empieza en 0.

• Si se quieren comparar dos gráficas, las frecuencias deben ser RELATIVAS. Cuidado si hay muchas categorías, en ese caso es mejor el histograma.
• Pictograma: No aporta información, sino que ayuda a visualizar.

4. Variables cuantitativas.

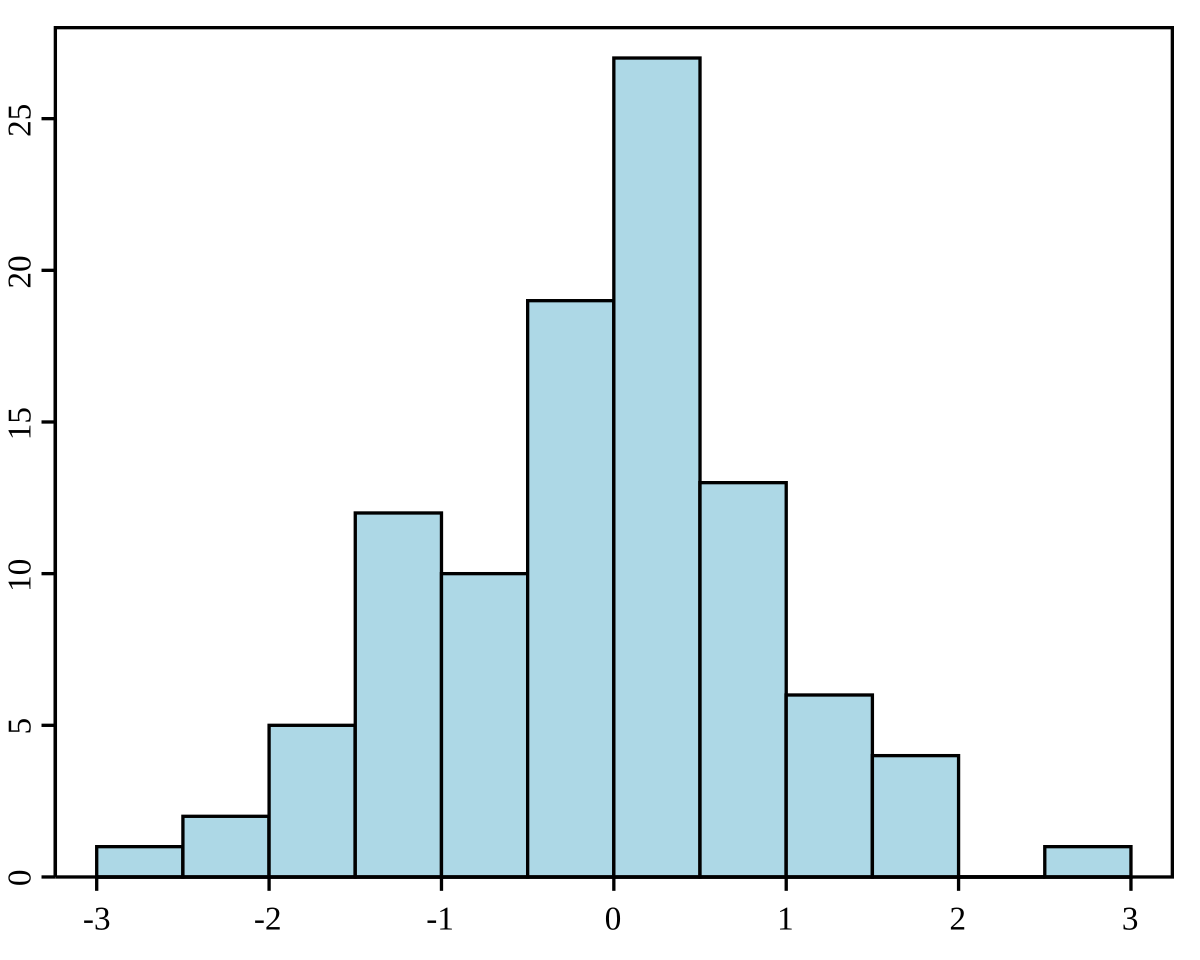
• Histograma.
• Rectángulos contiguos.
• Variable continua con datos agrupados en intervalos.
• Base de cada rectángulo = amplitud de cada intervalo. Altura determinada por frecuencia.

• Cuidado con confundir con diagrama de barras o con no tener en cuenta las amplitudes de los intervalos.
• Gráfico de troncos (o tallo) y hojas: híbrido entre tabla de frecuencia e histograma. Muestra distribución y valores de la variable.

• Gráficos para datos bidimensionales: No se puede representar más de una variable en el mismo gráfico.
• Gráficos de tendencias temporales:

• Diagramas de dispersión (nube de puntos o (scatter plot): Para representar dos variables continuas, donde el eje X = variable independiente y el eje Y= variable dependiente. La imagen nos muestra una posible correlación entre las variables.

• Diagrama de estrellas: para representar variables cuantitativas y comparar entre diferentes unidades. Cada variable =vértice del polígono.

Resumen Tema 5: Estadísticos univariables: medidas resumen para variables cuantitativas.

1. Resumen numérico de una serie estadística.

3 tipos de medidas estadísticas:

• Medidas de tendencia central: Muestran una idea general acerca del resto de valores.
• Medidas de dispersión o variabilidad: Información acerca de la heterogeneidad u homogeneidad de nuestras observaciones.
• Medidas de posición: se ordena un conjunto de datos de menor a mayor.

2. Medidas de tendencia central.

• Media aritmética o media (x): En poblaciones se representa con μ.
• La calculamos en variables cuantitativas. Fórmula:

• Mediana: observación de forma que 50% = datos menores, 50% = datos mayores.
• Si el nº observaciones es impar, valor de observación = (n/2)+1.
• Si el nº de observaciones es par, hay que hacer media entre (n/2) y (n/2)+1.

• Moda: valor que más veces se repite.Si hay dos = bimodal, si hay más de dos = multimodal. Sirve para variables cuantitativas y cualitativas.

3. Medidas de posición

Medidas que permiten ubicar el valor en una posición. Para variables cuantitativas. De menor a mayor:

• Cuantil: medida más general. Se representan mediante Q1, Q2, Q3... Los más usuales:
• Percentil: divide la muestra en 100 partes.
• Decil: Divide la muestra en 10 partes.
• Cuartil: Divide la muestra en 4 partes.

4. Medidas de dispersión.

También llamadas de variabilidad.

• Rango o recorrido: Diferencia entre valor mayor y menos.

• Desviación media: Media aritmética de las distancias de cada observación con respecto a la media de la muestra.

• Desviación típica o estándar: Cuantifica el error que cometemos si solo se usa la media. No puede ser superior a la media.

• Varianza: Desviación típica al cuadrado. 
• Recorrido intercuartílico: diferencia entre tercer y primer cuartil.
• Coeficiente de variación: Para comparar heterogeneidad de dos series numéricas con independencia de las unidades medidas. Valores entre 0 y 1. C.v. = s/media

5. Resumen numérico de una variable continua.

Estudio multicéntrico.

6. Distribuciones normales.

También llamada de Gauss. La función de densidad tiene forma de campana, y es simétrica.

Asimetrías y curtosis.

• Asimétrica hacia la izquierda (o negativa)= grado de asimetría < 0.
• Simétrica = grado de asimetría = 0.
• Asimétrica hacia la derecha (o positiva) > 0.

Curtosis o apuntamiento.

Para medir el grado de concentración de valores en torno a su media.

• Leptocúrtica = grado de curtosis > 0. Elevado grado de concentración en torno a los valores centrales.
• Mesocúrtica = grado de curtosis = 0. Concentración media en torno a los valores centrales.
• Platicúrtica = grado de curtosis < 0. Reducido grado de concentración en torno a los valores centrales.